Don't throw away your meter just yet! It might be fine! It might be telling the truth...
I'll get to the reason why down below, but first some necessary background:
I mentioned the "A" and "C" scale issue briefly in the recent "Step 3" of the "How to design your studio" series, here:
Deciding on isolation for your studio... But basically, you have to always use the same scale for everything, because it is impossible to compare readings taken on different scales, and it is impossible to convert between scales. (And considering that we are mostly interested in LOUD things in studios, we always use "C".)
I say "impossible" as in "mathematically invalid": it makes no sense to do that, as you would be comparing entirely different things, so it would be meaningless. And since we have to use the "C" scale to measure loud things (because "A" is not sensitive to low frequencies), then we also have to use "C" for measuring quiet things, even though our own hearing is not very sensitive to low frequencies at low levels.
This all relates to a couple of guys, by the names Fletcher and Munson, who did some research years ago, to see how sensitive we humans are to different frequencies. They originally expected that they would be able to draw a simple curve that showed a more or less fixed relationship between sensitivity and frequency.... but instead they found that our sensitivity curve changes, depending on how loud the sound is!
So we have one sensitivity curve for very quiet sounds, and a very different curve for loud sounds... plus a whole bunch of other curves in between.
This is what they found:
That's the famous set of "Fletcher-Munson" curves. As you can see, for loud sounds, we hear most frequencies at similar levels. If you look at the curve at the 100 dB level (also called the "100 phons curve" .... I'll get to phons in a bit), then you'll see that a sound at 1kHz and a sound at 100 Hz and even one at 30 Hz, we perceive them all as being the same subjective loudness, but a sound with a tone of 5 kHz would actually need to be 10 dB
quieter (only 90 dB real level) for us to judge that it is the same volume as the 1 kHz and 100 Hz and 30 Hz sounds. In other words, the curve is sort of "upside down" since it shows the inverse of "sensitivity". What it really shows is: "How loud does each frequency need to be, such that a human would judge that it is the same level as the reference sound?".
So: each curve in that graph shows the "equal loudness" contour for the reference sound, which is 1 kHz, but using a different reference level for each curve. In fact, that's pretty much how they figured this out! They would play a pure tone at 1 kHz and 100 dB, then ask people to turn up or down the level of
another tone played at the same time, but with a different frequency, until they thought it was the same level as the 1 kHz, 100 dB reference tone. Then they would measure the REAL level of that second tone, and plot it on the graph. They did that for a whole bunch of different frequencies, asking people to match the 1 kHz tone, they they drew the graph that shows the REAL level of each frequency, that average people said was the same loudness as the reference tone. (Then they did that all over again, but with the reference level at 90 dB... then repeat again at 80 dB... etc. For all possible sound levels, in 10 dB steps, and all possible frequencies [also in steps]).
OK. so for loud sounds, we hear them all roughly the same, except around 5 kHz where our ears are most sensitive.
But it's a different story for QUIET sounds: Go down to the curve labeled at the 40 dB level (the "40 phons" curve... see below), and you'll notice that a tone at 100 Hz would now need to be about 10 db LOUDER in order for us to judge that it is the same level as a tone at 1 kHz. And a sound at 50 Hz would need to be nearly 20 dB louder for us to judge that is the same as the 1 kHz tone. For a 30 Hz tone (roughly the lowest note on a 6 string bass), that would need to be 40 dB louder for us to judge that it is the same level!
Conclusion: our hearing is all messed up! It is not linear! We are more sensitive to some sounds than others, and it changes with both level and frequency.
Now for "phons". That's just a name that they invented to put on the curves, to make it easy to talk about them. The "40 phon" curve, is the one referenced to a tone of 1 kHz played at 40 dB, and shows how loud all other frequencies need to be, for us to say that they are exactly as loud as that "1 kHz 40 dB" tone. In other words, it shows the "equal loudness" curve for a 40 dB level. If you could set up a synthesizer to play every single possible frequency, with each one at the exact level indicated by that curve, then a typical human would say that each note you played is exactly as loud as any other note. Any specific frequency "Mr. Joe Average" listened to in that situation, he would say that it was the same level as any other frequency. So as you played notes up and down the scale on that hypothetical synthesizer, every note would sound as loud as any of the other notes.
So, getting back to sound level meters: the "A" weighting curve is an approximation of the 40 phon curve, and the "C" weighting curve is an approximation of the 100 phon curve. That's it. It really is that simple. (To be more accurate, the "A" weighting curve is the INVERSE of the 40 phon curve, and the "C" weighting is the INVERSE of the 100 phon curve.)
That's why we use "C" weighting to measure loud sounds, and "A" weighting to measure quiet sounds. Just remember: " 'A' = 40 phon, 'C'=100 phon", and you have the entire picture.
Here are the actual "A" and "C" weighting curves:
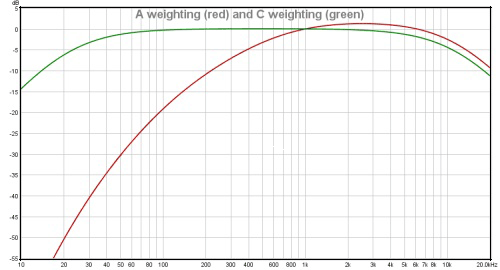
- SPL-DB-Weightings--A-and-C--GOOD!!!!.gif (36.85 KiB) Viewed 37044 times
- SPL-DB-Weightings--A-and-C--GOOD!!!!.gif (36.85 KiB) Viewed 37044 times
Flip those upside down, and you can see that they are both reasonable approximations of the 40 phon and 100 phon curves. Like this:
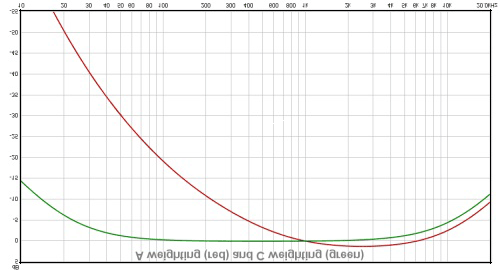
- SPL-DB-Weightings--A-and-C--flipped-upside-down-GOOD!!!!.gif (38.08 KiB) Viewed 37044 times
- SPL-DB-Weightings--A-and-C--flipped-upside-down-GOOD!!!!.gif (38.08 KiB) Viewed 37044 times
OK, so, now for the "impossible" part: You CANNOT validly compare measurements that you took using "A" weighting with other measurements that you took using "C" weighting.... because they measure different things! After you take the readings, there is no way to determine what the actual set of frequencies was that you measured! All you have is a number. So if you measured some music on "C" weighting, and got 70 dB on the meter, from just that number you have no idea if there was a lot of bass in there, or no bass at all! If you then take another reading some other place but using "A" weighting, and it happens to show 70 dB, you CANNOT say that they both show the same sound intensity! Because it is quite possible that the first one had a bass guitar in it, while the second one had only a flute in it. If you go back and measure the first one again, but using "A" this time, you might get a level of only 50 dB, instead of 70. And if you go measure the second one on "C" this time you might get 73 dB, instead of 70. Since there is no way of knowing what the individual frequencies were in each case, it is impossible to compare "A" with "C". They would both show exactly the same level if you measured a pure 1 kHz sine wave (because 1 kHz. is the reference point), but they would show very different levels for any other frequency, or combination of frequencies.
You also cannot convert between the two, for the same reason: the single number "85.3 dBC" tells you nothing at all about what the frequencies were that you measured, so there is no conversion factor you can apply, to convert that into dBA. This is not like converting between kilograms and pounds, or between miles and kilometers: those are easy, with a simple conversion, because they measure the same thing. But not with weighted sound level scales.... there is no way to convert. You are not comparing apples with oranges here! It's more like comparing "fruit" and "seafood"...
So: Since it is impossible to compare or convert readings taken on "A" with readings taken on "C", and since studios are all about "LOUD MUSIC", we studio people have to always use "C" weighting.
Actually, there a bit more to it than that: it turns out that Mr. Fletcher and Mr. Munson were optimists: later research showed that they were mostly right, but not quite. The situation is a bit worse than they thought. So today we use slightly different curves, just known as the "equal loudness curves". Here's a graph showing both the original "Fletcher-Munson" curves (blue color), and also the modern "Equal Loudness" curves (red color):
OK, now, getting back to the reason why Trevor is seeing things that he can't hear: The answer is simple: "Fletcher-Munson"!
Trevor has his meter set on "C" and it is showing sounds at levels of maybe 40 or 50 dB, that he doesn't consciously notice. You'd expect to hear such sounds, because you'd think that "50 dB is loud"! Except that Fletcher-Munson shows that really you should NOT expect to hear such sounds, if they are both quiet and at low frequencies: The
meter will detect them, but
you won't... For example, a 50 dB sound at 30 Hz is not audible to humans!
Surprise! The bottom line on those graphs shows the "threshold of hearing". Anything below that, is inaudible. And a 30 Hz tone has to be at least 50 dB, and probably close to 60 dB before you can hear it. Especially if there is a little background "ambient" noise going on that could mask such a quiet sound. Also, do take into account that most people would consider the 30 phon curve to be "very quiet" already, and the 20 phon curve to be "silent" (unless they have sensitive hearing).... So compare that graph again: Even a relatively high 50 Hz tone would have to be above 60 dB, and maybe 70 dB, in order to be audible for most people. A 100 Hz tone needs to be over 50 dB to rise above the 20 phon curve.
This is very surprising for most people, even musicians and sound engineers, because we don't ever notice those differences in normal life! By the very nature of our hearing, we CANNOT hear those things! So we assume that they don't exist, because we can't hear them. But the meter can hear them, even though we can't, so it is showing the presence of low frequencies that you can't hear. That might well be a distant truck, someone walking on the floor upstairs way across the other side of the house, or wind, or distant aircraft, or even distant music that is bass-heavy.
Which gets to the next point: if we can't hear it, does it matter? You might think that if you can't hear those low-level. low frequency sounds, then they don't matter and you can ignore them... But that isn't true for a simple reason: your mics CAN still hear them, even though you can't! And therefore those low frequencies WILL get into your recording sessions... they will modulate the higher frequencies, much like AM radio transmission carriers are modulated by lower audio frequencies. So those low-level "inaudible" things will appear in your tracks. They will "ride on top of" the other sounds. Thus, if you play a pure note on a guitar, it will no longer be pure, because the "distant truck" will modulate it... and now it will be audible! Even though it was not audible by itself, when combined with something else, it becomes audible. Both to your ears, and also in your mics. Especially in your mics, because they work very differently from how your ears work.
So, ... that's the reason why your meter is showing you things that your ears can't notice, and why you have to always use "C" weighting for all your measurements, even though measuring quiet things will show numbers that you can't hear....
Now, the good part of all this, is that pretty much all noise regulations require that the measurements must be done using "A" weighting, not "C"! So if the cops show up at your studio one day with a noise complaint from your neighbors, they will HAVE to measure the levels using "A", because that's what the law says. Thus, even though you KNOW that the level outside your studio is 50 dBC, it will likely only be 40 dBA, because "A" is less sensitive to low frequencies.. such as drums, bass, growling electric guitar, roaring keyboards.... Thus, you have an advantage. The only time you should set your meter to "A" is if the cops show up saying you are too loud. You can then validly, and legally, and correctly, measure the true level outside your place, and compare that to the regulations. The number on "A" will be lower than on "C", but that's the correct way to measure low levels anyway... which is why the law specifies it for ambient readings.
- Stuart -
Translate This Page
), and I will obviously re-test when the real meter comes in...but I did a test with Decibel X (an app for my iPhone 11) and here are the readings (C/slow):
I guess I just gotta do the best I can with it.
